Comonadic components

Comonadic Components

Now that we've introduced the basic idea of what a component is in Iodine, let's take a look at how comonads ome into the picture. For those not interested in the theory, continue on to the subsections of this section to see some examples of how this can be used.

A comonad is a mathematical concept from category theory which has found many application in both theoretical computer science and practical programming applications.

Like many abstract mathematical concepts, comonads can be thought of in many ways. For our purposes here, comonads can be thought of as an abstraction of somthing that:

1. Holds onto a state.
2. Has a way of updating that state.

For a more in-deth explination, and similar view of comonads, see Comonads as Spaces. In Iodine, a Comonad is defined as a container F with methods:

interface Comonad<W>: Functor<W> {
    val state: Hk<W,S>.S
    fun Hk<W,S>.duplicate(): Hk<W,Hk<W,S>>
}

where state gets the current state of the comonad, and duplicate encodes a way of denoting possible "future states" (how this is accomplished will be more clear later, with some concrete examples).

A comonadic component then, is a component whose internal state and state transitions are modeled via a comonad. As it turns out, all components in Iodine are in fact comonadic -- but to avoid added complexity, this fact is hidden from the user unless they would like to explicitly explore this approach to modeling user interfaces.

Store Components

One of the most basic examples of a comonad is the Store comonad. The type itself is defined as follows:

data class Store<X, S>(
    val internalState: X,
    val view: (X) -> S
)

Essentially a store is something that holds onto an internal state X, and "exposes" a computed view of that state with the supplied function. For instance:

data class Person(
    val name: String,
    val age: Int
)

val personNameStore = Store(
    internalState = Person("Bob", 42),
    view  = { person -> person.name }
)

The state of a Store is just applying the view to the internalState to get the publicly exposed state:

val Store<X,S>.state: S = view(internalState)

The duplicate operation is defined as follows:

fun Store<X,S>.duplicate(): Store<X,Store<X,S>> {
    val currentStore = this
    return Store(
        internalState = currentStore.internalState,
        view = { nextState -> 
            Store(
                internalState = nextState,
                view = currentStore.view
            )
        }
    )
}

So in other words, if we view a duplicated state with a new internalState, we get an updated Store that "stores" that new state, with the same view as before. This is how duplicate can be used to transition a Store to a new state. The method for updating the state of a Store is to just pass in a new internal state.

Thus, a StoreComponent is just a component holding on to some state S that can be updated to any value. There are no complicated state transitions to contend with. For this reason, StoreComponents are good at modeling things like basic entry forms that just "hold on" to some entered value.

In fact, by exposing the internal state, together with the "viewed" state -- we can take another perspective on comonadic store components entirely by viewing these parameters as the type of inputs and outputs to the component -- A, B.

This turns out to be the most useful application of Store components in Iodine -- so we give a name to this concept: A Form. Exposing these two parameters rather than simply an input parameter, as is done with normal Iodine components gives us an instance of another important mathematical struture -- that of the Profunctor. This is all explained in greater detail, with examples, in the section on Forms.

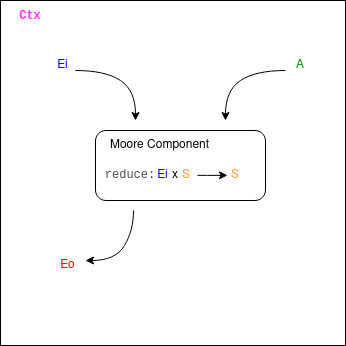
Moore Components

Our next example allows for the modeling of some more complicated state transitions in a Component, and actually corresponds to something close to the original design of Iodine -- as well as being similar to the Elm Architecture.

The Moore comonad -- so named because it acts similarly to a finite state machine called a Moore machine -- is defined as follows:

data class Moore<E, A>(
    val value: A,
    val next: (E) -> Moore<E, A>
)

So again, a Moore comonad holds on to a "current state" with value. However, unlike the Store comonad, it also comes equipped with a transition function next which depending on an event E, will return a new state of the Moore machine (Moore<E, A>) according to the event passed in.

Note that the "event" here is different from the usual E parameter of an Iodine Component, which is a type of event that the component can asynchronously output -- so to distinguish between the two, we use the convention of Ei as a "input event" and Eo as an "output event".

Let's look at a simple example of defining a component using this type of architecture defined by the Moore comonad:

/**
 * The Elm Arctitecture (a.k.a. Model-View-Update) in Iodine.
 *
 * Compare with https://elm-lang.org/examples/buttons
 *
 */

// Model
value class Model(val count: Int)

enum class Msg {
    Increment, Decrement
}

object CounterComponent: MooreComponentImpl<IodineContext, Msg, Void, Model, Model>(
    initialState = Model(0)
) {
    // View
    @Composable
    override fun C.render(state: S) {
        Column {
            Text("Hello MVU!")

            Button(text = "-", onClick = { emit(Msg.Decrement) })
            Text(state.count.toString())
            Button(text = "+", onClick = { emit(Msg.Increment) })
        }
    }

    // Update
    override fun reducer(event: Msg, state: Model): Model =
        when (event) {
            Msg.Increment -> Model(state.count + 1)
            Msg.Decrement -> Model(state.count - 1) 
        }
}

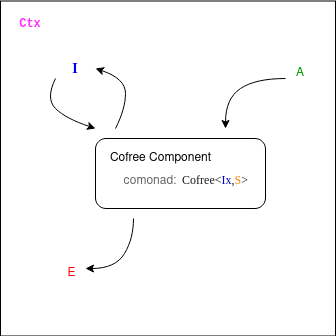
Cofree Components

The most flexible of the comonadic components defined by Iodine is that of a Cofree component. Unlike the other comonads we have seen, Cofree takes a higher-kinded parameter F:

data class Cofree<F, A>(
    val state: A,
    val next: Hk<F, Cofree<F,A>>
)

Again, like the others, a Cofree holds on to a state -- but it's next parameter takes an an application of F to control how the "next states" branch out.

Combining Components

So far, all of the types of comonadic components we have seen all have concrete representations as interfaces or abstract classes in the core iodine package. What then is the use of having a generic ComonadicComponent interface hanging around (besides just being good fun and interesting for those who enjoy Category Theory)?

The answer lies in the different ways that one can combine comonads. As a bit of a teaser, you can think of a complex combination of comonads as giving you something similar to a statically-typed version of a UI testing framework like Selenium or Espresso. To begin, meet Day:

interface Day<F,G,A>: Hk<Day.W<F, G>, A> {
    class W<F,G>

    fun <B,C> runDay(x: Hk<F,B>, y: Hk<G,C>, f: (B,C) -> A): A
}

If this implementation doesn't make sense -- that's fine! It'll probably take some time playing around with examples to get an intuition for how this works "under the hood" -- but at a high-level: Day gives us a way of embedding two comonads F, G into a larger comonad Day<F,G> where at any point in time, you can manipulate the state of Day<F,G,S> by either making use of the API provided by F or by making use of the API provided by G.

Testing a Comonadic API

Now that we've seen a few different ways of combining comonadic components -- let's look at some examples of how we can use these ideas in testing.

Let's say you're building an app for managing recipes, and you want to build an automated UI test to see what happens when you try to add a recipe with the same name as one that you already have saved.

This App's main activity can be broken down into two high-level components -- a MyRecipeAppBar and a MyRecipesView. Let's look at what sort of APIs they provide.

object MyRecipeAppBar: ComponentDescription<ActivityCtx, MyRecipeAppBar.Action, MyRecipeAppBar.Event, Unit> {
    interface Action {
        /** Add the given recipe to the app. */
        fun addRecipe(recipe: Recipe)
        /** Navigates the user to the preference activty. */
        fun openPreferences()
    }

    sealed interface Event {
        /** 
         * Event emitted whenever a recipe is imported into the app.
         *
         * Examples: 
         *   User manually enters in a new recipe.
         *   User imports a recipe via the "share" feature of another app.
         */
        data class OnRecipeAdded(val recipe: Recipe)
    }

    ...
}

object MyRecipesView: ComponentDescription<ActivityCtx, MyRecipesView.Action, Void, Unit> {
    interface Action {
        /** Sort the list of recipes in the app by the given strategy. */
        fun sortRecipes(by: SortingStrategy)

        /** Get the list of recipes in the view in the current sorted order. */
        fun getRecipes(): List<Recipe>

        /** Remove a recipe from the app. Returns false on failure. */
        fun removeRecipe(recipe: Recipe): Boolean
    }

    ...
}